View on GitHub

logic-texts

Repositório de textos da disciplina de lógica UFCG

Outros Sistemas Dedutivos (Lógica Proposicional)

Por ora, vimos dois métodos de verificação de propriedades de fórmulas (validade e satisfazibilidade) e argumentos (validade): tabela-verdade e árvores (Tableaux). Em geral o Tableaux Semântico pode ser considerado tanto como um algoritmo (um pouco) mais eficiente que a tabela verdade, mas também um sistema dedutivo. Como vimos anteriormente, um sistema dedutivo tem as seguintes características:

Na verdade, vários outros exemplos de sistemas dedutivos foram desenvolvidos ao longo de história, que funcionam para vários estilos de lógica, clássicas ou não. Neste módulo, faremos um breve passeio por alguns deles, entendendo seus pontos fortes e suas limitações.

Antes de começar, deixa eu revisitar o que devemos entender como prova formal em um sistema dedutivo. Na lógica, primeiro precisa existir um conjunto específico de símbolos a partir dos quais construímos uma prova — os símbolos de uma linguagem lógica, como a lógica proposicional, por exemplo, junto com alguns símbolos adicionais para organizar a prova. Qualquer sequência desses símbolos pode ser então uma candidata a receber o título de prova; pode ainda não ser, dependendo de uma verificação. Segundo, deve haver um procedimento de decisão para determinar, dentro de um tempo finito, se uma sequência candidata a prova é realmente uma prova — algum tipo de algoritmo que recebe a prova candidata como entrada e retorna sim ou não. O procedimento deve então ser preciso, para que não haja dúvida sobre a resposta. Desta forma, as provas precisam também ser finitas, algo que é intuitivamente correto: nenhum algoritmo pode ser finito verificando algo infinito.

Vamos verificar, como exemplo, o método de prova com árvores (Tableaux). A sequência de símbolos é a lógica proposicional, adicionada de símbolos gráficos, como traços e números, que ajudam a desenhar a prova. Como estamos sempre lidando com fórmulas com um número finito de átomos e conectivos, o número de nós da árvore nunca será infinito, consequentemente a árvore terá um número finito de caminhos. Assumindo isso, temos um procedimento de decisão preciso que sempre termina, pois verifica se, para cada caminho, o mesmo está aberto ou fechado. Desta forma, podemos classificar a árvore do Tableaux como um método de prova formal para satisfazibilidade da lógica de predicados.

Vamos dar uma olhada aqui nos seguintes sistemas dedutivos, que fornecem meios de realizar provas formais na lógica: axiomático e dedução.

Sistemas Axiomáticos

Começo novamente resgatando as árvores do Tableaux: todas elas trazem informação sobre satisfazibilidade apenas. Se a árvore tem apenas caminhos fechados, o conjunto de fórmulas na raiz é insatisfazível; se algum caminho sobrar aberto, há pelo menos um caso (modelo) para satisfação. Assim, é natural dizer que a principal noção de provas em árvores é a satisfazibilidade de um conjunto de fórmulas.

Por outro lado, em sistemas axiomáticos de prova (também conhecidos como sistemas de Hilbert ou Hilbert-Frege), a noção é provar a validade de uma fórmula. Sim, uma fórmula apenas; nesses sistemas, queremos verificar se uma fórmula é sempre verdadeira. Vou mostrar um primeiro exemplo de prova axiomática, e ir explicando aos poucos os componentes.

Suponha que queremos demonstrar se a seguinte fórmula (¬P → P)→ P é válida. Ajuda saber, já já explico por quê, que ela é sim válida, por isso é seguro tentar a prova. Para começar, temos que ter um lugar de onde partir, para começar essa prova, algumas afirmações que sabemos ser válidas sempre, uma base de lançamento segura. Fórmulas que sabemos ser válidas independente de outras, essas vamos chamar de axiomas. Querem ver três exemplos de axiomas?

(A1) α→(β → α)

(A2) (α→(β →γ ))→((α→β)→(α→γ))

(A3) (¬β →¬α)→((¬β →α)→β)

Parecem complicadas, eu sei. Atentem-se para A1, que é a mais fácil, considerando aqui que α e β representam uma fórmula qualquer bem-formada na lógica proposicional (ficou convencionado na lógica de que letras gregas representam fórmulas). Assim, em A1, se você colocar uma fórmula qualquer do lado esquerdo de uma implicação, e do lado direito colocar qualquer outra fórmula implicando na primeira novamente, isso sempre será verdade. Se α=p∨ q e β=q, é só conferir: (p∨ q)→(q→(p∨ q)) só tem modelos na sua tabela verdade - todas as interpretações são verdadeiras.

Se tivermos algumas fórmulas iniciais pra começar, precisamos tentar chegar, a partir delas, na fórmula que queremos provar como válida. Faremos isso através de algumas transformações sintáticas nas fórmulas, e teremos certeza de que as transformações são corretas é através de regras de inferência. Olha aí um exemplo, que a gente chama tradicionalmente de Modus Ponens, do latim para “Modo de Afirmar”.

Regra (MP):

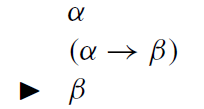
outros_estilos/t1.png

Na regra, α e β são, novamente, qualquer fórmula. Antes do triângulo, temos as entradas da regra, e depois, a saída, o resultado. Aqui, leia-se: se uma implicação for válida, e o lado esquerdo dela também for, então podemos gerar uma nova linha na prova, com o lado direito dessa implicação sozinho. Os três axiomas que mostrei acima, mais a regra MP, formam um sistema axiomático, e já dá para explorar algumas provas com esse sistema bem pequenininho.

Abaixo, usando esse sistema, mostro como podemos estruturar uma prova no método axiomático. Começamos usando os axiomas A1 e A2, substituindo α,β,γ com fórmulas que parecem ser úteis para esta prova específica.

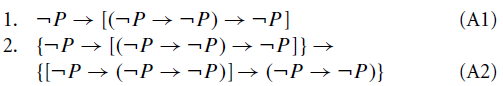
outros_estilos/t2.png

Por exemplo, na linha 1, escolhemos α=¬P e β=(¬P →¬P). Já na linha 2, podemos ver a aplicação de A2 como uma distribuição da implicação com α=¬P, β=(¬P →¬P), γ=¬P.

Continuemos com a prova seguindo o estilo axiomático. A partir das Linhas 1 e 2, podemos aplicar a regra MP para chegar a uma nova fórmula, em uma nova linha, também válida.

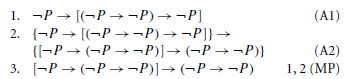
outros_estilos/t3.png

O resultado é outra implicação! Assim, podemos tentar usar novamente axiomas para aplicar de novo MP, até chegarmos ao resultado que queríamos demonstrar: (¬P →P)→P.

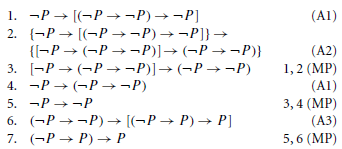
outros_estilos/t4.png

A partir do exemplo, conseguimos estabelecer algumas ideias gerais de uma prova formal axiomática; ela é uma sequência de fórmulas bem formadas, em que cada fórmula dessa sequência ou é um axioma ou o resultado de aplicação de uma regra de inferência, usando como entrada algumas fórmulas anteriores na sequência. A prova da validade de uma fórmula têm esta como última fórmula da sequência. Se existe uma prova formal para uma fórmula α dentro de um sistema axiomático A, então α é um teorema do sistema A; simbolicamente, ⊢A. O símbolo ⊢ reflete uma prova formal, sintática, de um teorema ou argumento (compare com vinculação semântica, símbolo ⊧).

Com isso, podemos definir duas propriedades de um sistema dedutivo: solidez e completude. Um sistema A é sólido se apresenta a seguinte propriedade: se ⊢A α então ⊧A α. Isso significa que se há uma prova da validade de uma fórmula α nesse sistema, ela é correta (realmente α é uma tautologia, ou teorema). Por outro lado, um sistema A é completo se apresenta a propriedade: se ⊧A α então ⊢A α. Isso define que se uma fórmula é um teorema, é possível provar isso no sistema (temos axiomas e regras de inferência suficientes).

Até agora, tudo ok. No entanto, fica difícil de acreditar que o sistema axiomático que apresentei acima é sólido e completo para a lógica proposicional; por exemplo, não dá para provar P ∨ ¬P, já que nenhum dos axiomas pode lidar com disjunções. Isso nos leva a discutir um ponto importante. É interessante manter um sistema de prova simples, minimizando o número de axiomas e regras; por isso, é muito comum confinar a linguagem aceita pelo sistema a uma porção restrita da linguagem completa.

Por exemplo, sabe-se que {→,¬} é um conjunto núcleo (core) de conectivos da lógica proposicional! Quer dizer que qualquer fórmula nessa lógica pode ser representada apenas pode esses dois conectivos. Olhem as equivalências abaixo que permitem fazer isso:

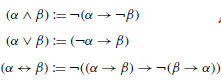
outros_estilos/t5.png

Então, para mostrar que P ∨ ¬P é válido, basta transformá-la em (¬P →P)→P, e então…opa, já mostramos isso, não é? As primeiras cinco linhas da prova axiomática anterior fazem exatamente isso. Enfim, o sistema apresentado, mesmo minúsculo, é completo e sólido para a lógica proposicional.

Por fim, quero mostrar o uso deste sistema axiomático para demonstrar a validade de um argumento. Neste caso, as premissas são consideradas como assumptions (A na figura abaixo), colocadas como fórmulas válidas na prova, junto com axiomas e resultados da aplicação de regras. Aqui, demonstramos que o argumento p→q,q→r⊢p→r.

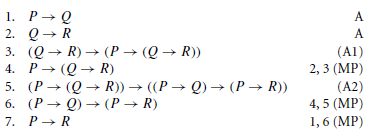
outros_estilos/t6.png

Dedução Natural

Já repeti algumas vezes, mas vou voltar novamente a uma mesma ideia: verificar a validade de um argumento é o que interessa em lógica. Tudo que você viu e vai ver gira em torno desta mesma tarefa. Um argumento informal poderia ser escrito assim:

O programa calcula o número de disciplinas cursadas e calcula o CRE do aluno. O programa foi feito em Python. Portanto, o programa calcula o CRE do aluno e foi feito em Python.

Poderíamos codificar este argumento da seguinte forma, usando lógica proposicional:

Com a intervenção humana, podemos verificar um argumento por demonstração, muitas vezes de forma mais simples. Como provador, seu objetivo é transformar as premissas na conclusão, através de transformações sintáticas corretas. Essas transformações são corretas se seguirem a aplicação da mesma ideia que usamos em métodos axiomáticos – regras de inferência, que garantem a consistência das fórmulas resultantes da transformação de verdades anteriores. O estilo de prova chamado Dedução Natural é similar na ideia de gerar novas fórmulas consistentes com as anteriores; a diferença crucial é a dedução natural é mais aplicável, com apenas um sistema por linguagem, com regras definidas por conectivo. Além disso, apenas em sistemas naturais podemos fazer hipóteses temporárias (caixas), com essas hipóteses possivelmente sendo dispensada (discharged) quando o propósito da hipótese for atingido. Mais em exemplos em breve.

Este é um sistema de prova que reflete melhor nossa prática rotineira de raciocínio, por isso o chamamos de Natural. Iniciar com as premissas, ir gerando novas proposições, até chegarmos no resultado do raciocínio, a conclusão. Ao aplicar essas regras às premissas, esperamos que chegaremos a mais algumas fórmulas, e se aplicarmos mais regras a estas, em algum momento chegaremos na fórmula da conclusão.

Um sistema de dedução natural não possui axiomas. As regras são organizadas por conectivo, divididas entre regras de introdução e regras de eliminação. Vamos iniciar com as duas regras referentes à conjunção:

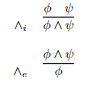
outros_estilos/t7.png

Uma regra deve ser lida de cima para baixo; acima do traço, temos as fórmulas de entrada da regra, necessariamente já conhecidas como verdadeiras, e abaixo do traço, temos a fórmula resultante da regra. Na regra de introdução da conjunção, se forem provadas como verdadeiras as fórmulas, podemos deduzir a conjunção entre os dois. Já na eliminação da conjunção, basta que se tenha como verdadeira uma conjunção de duas fórmulas, qualquer uma delas pode ser tomada como verdade, já que as duas são verdadeiras ao mesmo tempo.

Você deve estar achando essas regras bem fáceis, e nisso concordo com você. Ainda assim, saber aplicá-las exige um pouco mais de habilidade, e é neste ponto que eu quero exercitar a habilidade de dedução. Vamos voltar ao argumento de exemplo, reescrevendo-o para a utilização da dedução natural: d ∧ c, p ⊢ c ∧ p

Supondo que temos que realizar a prova de validade deste argumento, vamos montar o esquema de dedução, que é o primeiro passo para uma prova correta e organizada. Isso é importante, pois demonstrações são feitas para convencer outras pessoas por isso têm que ser precisas e claras. A primeira coisa é copiar as premissas, uma por linha numerada.

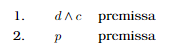
outros_estilos/t8.png

A ideia aqui é usar estas duas linhas como origem para transformações que vão gerar a conclusão. Acho importante você deixar um espaço e já escrever a conclusão, na última linha, mesmo sem saber ainda qual o número desta linha na prova completa.

outros_estilos/t9.png

Essa prática ajuda a saber onde queremos chegar, facilitando a definição da estratégia a utilizar. Olhando para a conclusão, você deve se perguntar: ``Qual o caminho mais apropriado para chegar a este tipo de conclusão?’’ O que chamo de tipo de conclusão consiste na estrutura da fórmula. Neste caso, a conclusão tem uma estrutura de conjunção – este é o conectivo principal da fórmula.

Voltando à nossa dedução, qual seria a melhor forma de chegar a uma conjunção? Que regras deveríamos aplicar para chegar lá? Como só vimos duas regras até agora, é simples: para chegar a esta conjunção (c ∧ p), precisamos chegar a cada um dos lados da conjunção isoladamente, para no final juntar os dois no resultado, utilizando a regra de introdução de conjunção. Você poderia já colocar estes dois lados nas linhas acima da conclusão, assim:

outros_estilos/t10.png

Agora nosso trabalho se resume a tentar deduzir c e p isoladamente. A proposição p já é premissa, então ela já é válida nesta dedução, por isso vou apagar.

outros_estilos/t11.png

O problema que resta é chegar ao c isolado. Você tem agora que olhar as premissas para tentar delas derivar o resultado desejado. Veja que na Linha 1 temos a conjunção cujo um dos lados é exatamente c, que eu posso extrair usando a regra de eliminação. A criação da nova linha exige uma justificativa, que fica do lado direito, incluindo o nome da regra e a linha de onde vêm as entradas da regra (nesta regra, só há uma entrada, a Linha 1):

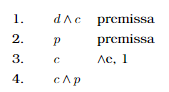
outros_estilos/t12.png

Temos os dois lados isolados na dedução, assim você pode finalizar a prova com o último passo de introduzir a conjunção. Como a linha já está colocada, falta apenas justificá-la como resultado.

outros_estilos/t13.png

Perceba que duas linhas foram usadas na justificativa, já que esta regra precisa de duas entradas (cada lado da conjunção). Um sistema de dedução natural para a lógica de predicados completo possui um número bem razoável de regras, pois cada conectivo e quantificador define duas regras, introdução e eliminação. Vamos nos limitar aqui a discutir regras para implicação, só para dar um gostinho de como se faz dedução com caixas.

Para a implicação, começamos do jeito mais simples, a sua eliminação (deixemos a introdução para depois, já que precisaremos de um conceito novo). A eliminação da implicação é definida assim:

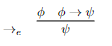
outros_estilos/t14.png

A eliminação da implicação nada mais é que a regra que já vimos no sistema axiomático, Modus Ponens (Modo de Afirmar). Nela, se sabemos ser verdade a própria implicação, e sabemos ser verdade seu lado esquerdo, com certeza o lado direito é verdadeiro. Uma outra regra que vamos adicionar é análoga a esta: Modus Tolens (Modo de Negar), que permite deduzir a fórmula do lado esquerdo de uma implicação quando tem-se como verdadeira a negação da fórmula do lado direito.

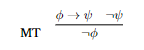
outros_estilos/t15.png

Aqui tem uma novidade: teremos agora como \textit{introduzir} uma implicação onde não existe uma. Lembre-se de que uma fórmula como p→q não afirma p nem q. Criar uma implicação em uma dedução exige que criemos \textit{hipóteses temporárias}, cujo efeito (escopo) é limitado a apenas um pedaço da dedução – um trecho dentro da lista ordenada de linhas numeradas. Este trecho temporário é representado por uma espécie de quadro de contorno sólido, uma caixa.

Vamos trabalhar em cima de um exemplo de argumento: ¬j → ¬c ⊢ c → ¬¬j

Vou começar escrevendo a premissa, seguida da conclusão no final. O espaço em branco entre elas será nossa área de trabalho, onde vamos pensar a estratégia.

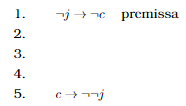
outros_estilos/t16.png

Nosso objetivo é chegar numa implicação, mas ela não existe na dedução ainda, vamos assim precisar criar de algum lugar. Vamos criar as condições para que uma implicação possa ser deduzida: vou assumir como verdadeira a fórmula esquerda da implicação desejada c. Não quer dizer que ela seja, talvez não seja, mas vou assumir como uma hipótese; já que não sabemos se ela existe, então a colocaremos dentro de um espaço temporário, onde as fórmulas anteriores também são verdadeiras, junto com essa hipótese. No final da caixa, queremos que esta hipótese seja dispensada (discharged).

outros_estilos/t17.png

É importante pensar que a caixa é uma sub-dedução dentro da dedução maior; neste caso, podemos usar Linhas 1 e 2 como verdade para a dedução dentro da caixa. Neste caso, se conseguirmos deduzir, no final dela, o lado direito da implicação desejada (¬¬j), chegamos à conclusão que queríamos; partimos, assumindo o lado direito, numa dedução que leva ao lado direito, ou seja,o lado direito foi realmente implicado a partir do lado esquerdo!

outros_estilos/t18.png

Perceba que nosso problema da caixa para fora está resolvido, basta agora resolver o miolo da caixa. Precisamos então, a partir das Linhas 1 e 2, chegar em ¬¬j. Mas, veja, o final da caixa, onde queremos chegar, é justamente o lado esquerdo negado da implicação da Linha 1! Se eu perguntar qual a estratégia para chegar na negação do lado esquerdo de uma implicação, você vai rapidamente me responder que precisamos usar Modus Tolens, de algum jeito. Para isso, precisamos negar duplamente c, e para isso existem regras triviais para introdução e eliminação da dupla negação.

outros_estilos/t19.png

Caixas como essas são usadas em regras para disjunção, negação e contradição, além de quantificadores; se tiver curiosidade, leia textos completos sobre dedução natural em: